A final-year mechatronics engineering student has proposed a new control systems model that could be used in applications from thermostats to cruise control to hearing aids.

Vishnuram Arumugam, 22, researched the control model over the past year, as part of his honours project.

The model replaces one mathematical equation with another – trading the integer-order differential equation typically used in automated control models, with the more general fractional-order differential equation.

“This is a more powerful model with less assumptions. It means we could have a more accurate prediction of how a room’s temperature varies over a period of time and then improve the actions a thermostat can take to keep the temperature at a steady level,” Arumugam says.

Arumugam began to form the seeds of his idea in his third year, after enrolling in Curtin’s Dynamic Modelling and Control Unit. Intrigued at applying his love of mathematics to a real-world application, Arumugam spent several hours each night searching the Curtin library catalogue for intricacies on control theory.

“What inspires me to study is the beauty and elegance of mathematics,” Arumugam says.

“I was particularly fascinated because control theory uses areas of mathematics I had studied before, but never thought of putting together. And because I really wanted to understand it, it was easy to spend a lot of time and effort on it.”

When Arumugam’s passion for control systems came to the attention of Curtin Associate Professor Lorenzo Ntogramatzidis, they formed a collaboration with Ntogramatzidis’s colleague, Dr Fabrizio Padula. Both members of staff supported Arumugam to take units in mathematics that weren’t in his curriculum so he could further his knowledge.

“He was doing perfectly on assessments and exams that he wasn’t enrolled even in. It was astonishing. Even then, I couldn’t really call myself his ‘mentor’ because I didn’t really feel like a mentor: I felt like we were at the same level,” Ntogramatzidis says.

Arumugam soon realised how other branches of mathematics could be used to improve control system functionality. The idea of using the fractional-order differential equation, something which only a few control systems engineers have otherwise proposed, greatly impressed Ntogramatzidis.

“Through his own hard work, he has been able to grasp incredibly abstract and difficult areas of mathematics. He has achieved a level of understanding far beyond his age and level of study.

“That’s something very few undergraduate students are able to achieve.”

Arumugam, Padula and Ntogramatzidis, are preparing a research paper on the model in collaboration with the University of Padua, Italy, which is due to be published within the next few months.

How does it work?

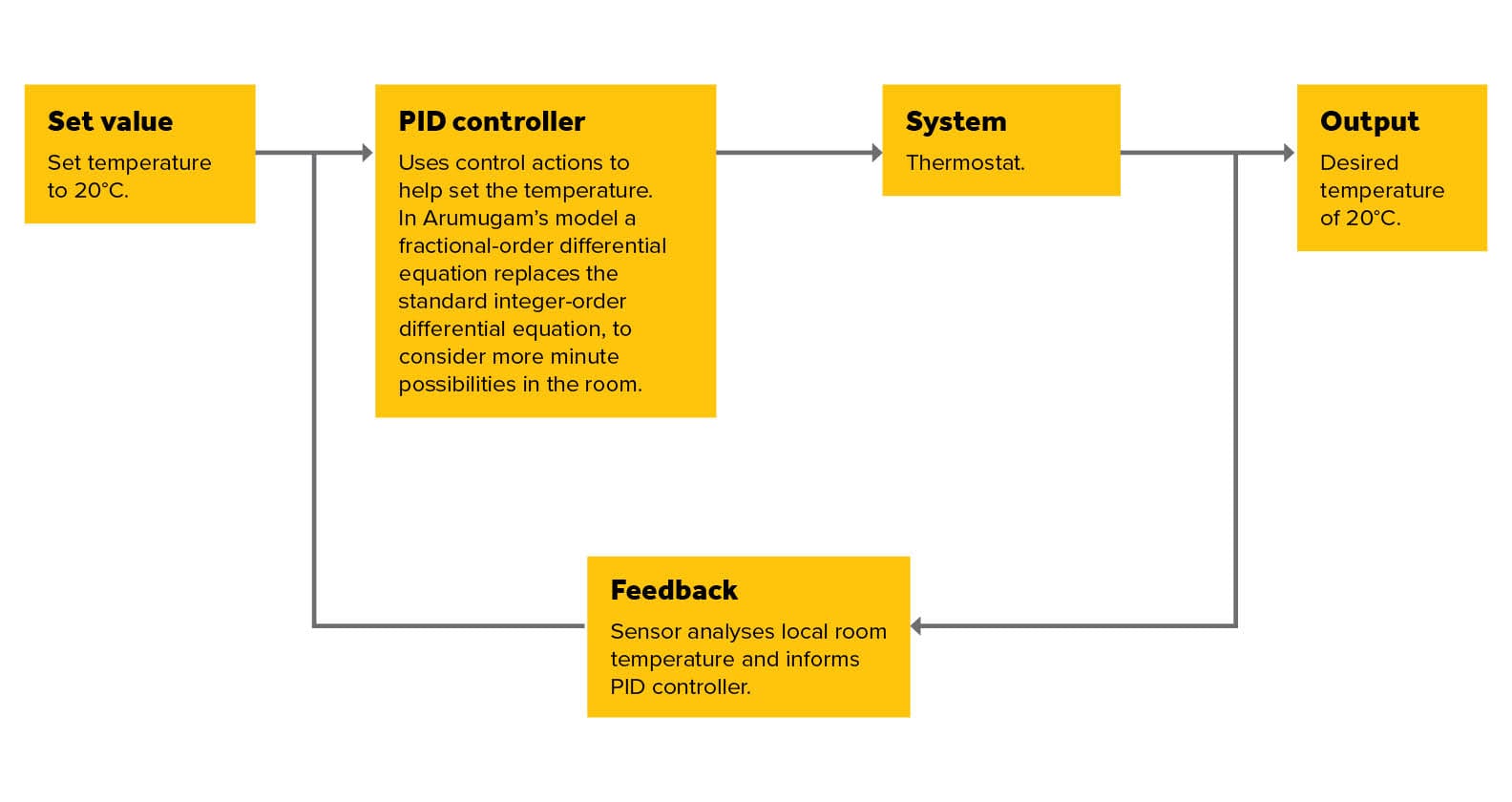
Control systems are the ‘brains’ behind automated technology and play essential roles in our daily lives. But they are not 100% accurate.

Until now, most control systems have been described in part by integer-order differential equations. These equations predict changes in the physical system that the technology operates in, such as a thermostat predicting temperature changes in a room to maintain the desired room temperature. But they have limited accuracy because they only involve integer-order derivatives, such as the first, second and third.

The model by Arumugam replaces one of the integer-order differential equations with a fractional-order differential equation, which accommodates for fractional-order derivatives, such as derivatives of order one-half or the square root of 2. This approach allows the model to describe phenomena more accurately than integer-order differential equations.

“It’s analogous to replacing a set of fixed length wrenches with an adjustable wrench,” says Arumugam.

If you want to find out more about Arumugam’s model, please contact Associate Professor Lorenzo Ntogramatzidis.

Interested in studying at Curtin? Read more about our undergraduate Bachelor of Engineering (Mechatronic Engineering).